CS231n Lecture 05. CNN - Convolution Neural Network

이미지 인식의 대표 알고리즘, 공간적 구조를 유지하는 CNN에 대해 알아보자

History of CNN

1957년, Frank Rosenblatt가 Mark I Perceptron machine 을 개발

 

최초의 퍼셉트론 형식의 기계 

• update rule 이 존재함 - back prop과 유사해 보이나 당시엔 단지 w를 사람이 직접 조절해 가며 맞추는 방식.

 

 

• 1960년, 최초의 Multilayer Perceptron Network 발명, NN와 비슷한 형식이나, 아직 back prop은 없었다. 

 

 

• 1986년 처음으로 network 학습 개념 정립 시작됨
• back prop 기법의 발견

 

 

 

• 2006년 Geoff Hinton 과 Ruslan Salakhutdinov의 논문이 DNN의 학습 가능성 선보임
• backprop이 가능하려면 세심하게 초기화를 해야 했음. - 전처리의 필요성 대두
•  초기화를 위해 RBM을 이용해 각 히든레이어 가중치를 학습시켜야 했음
• 이렇게 초기화된 히든 레이어를 이용해 전체 신경망 back prop / fine tune(이미 학습된 모델을 기반으로 내 목적에 맞게 변형하여 이미 학습된 모델 Weights로 부터 학습을 업데이트하는 방법) 해주는 방식

 

 

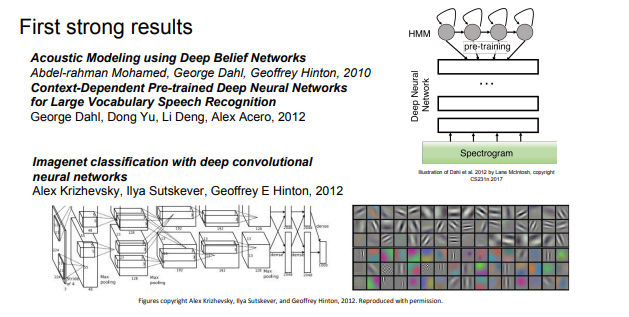
• 2012 비로소 NN 기법이 각광
• 음성인식 분야에서 높은 성능 보임
• 이미지넷 benchmark error를 현저하게 줄인 NN

 

 

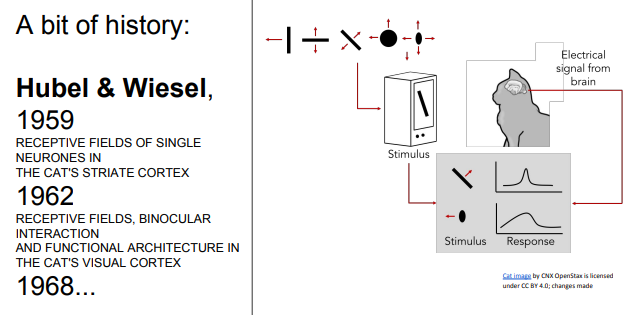
• 1950년대, Hubel & Wiesel의 1차시각피질 뉴련의 관한 연구 - 고양이 뇌에 전극을 꽂고 뉴런 관측
  • oriented edges, shapes같은 것에 뉴런이 반응한다는 사실 알아냄

 

 

 

• 실험결과
  •  피질 내 인접세포들은 visual field에 어떤 지역성을 띄고 있음. - 특정 구역에서 특정 시각적 자극에 반응(?) 

 

 

 

• 시각신호는 계층적 구조 지님!

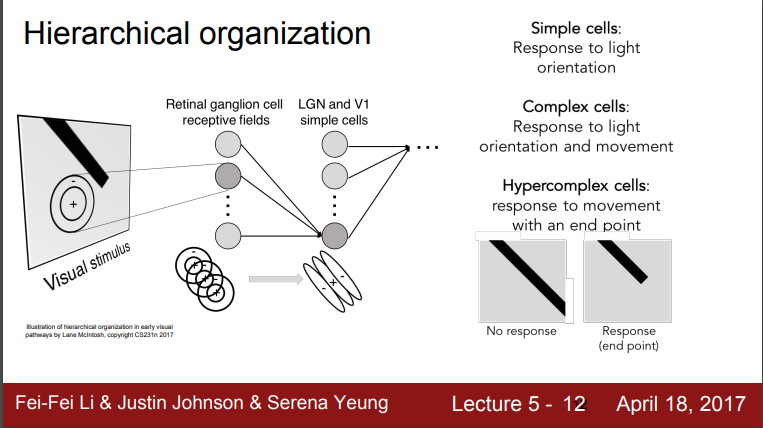
• Retinal ganglion cell에 가장 먼저 시각신호가 도달
• Simple cell에 가장 마지막으로 시각신호가 도달 - 다양한 edges의 방향과 빛의 방향에 반응
• Complex cell - 빛의 방향 뿐만 아니라 움직임에서 반응하는 cell, simple cell과 연결되어있음
• Hypercomplex cell - 끝 점과 같은 구체적 시각정보에 반응

즉 각각의 cell이 받아들이는 시각 정보가 다르다!!

-> 여기서 corenr나 blob에대한 아이디어를 얻음

 

 

 

 

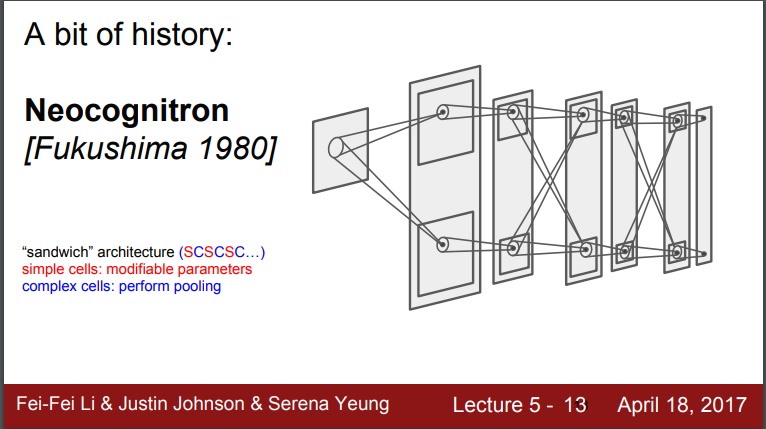
• Neocognitron - 1980년대,  Hubel, Wiesel이 발명한 최초의 NN - Simple,complex cells 아이디어 사용
• Fukushima가 simple/complex cell을 교차시킴
  • simple cell - 학습가능한 파라미터 가짐
  • complex cell - pooling 등으로 구현 - 변화에 보다 강인

 

 

 

 

 

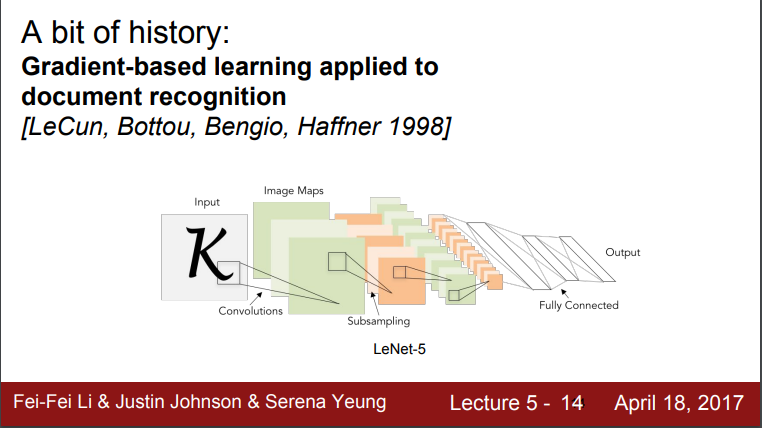
• 1998년, Yann LeCun이 최초로 NN 학습에 backprob과 gradient-based learning 적용
• 문서 인식에 굉장히 높은 인식률 보임 - 실제 우편번호 인식에 널리 쓰임
• 한계
  • 여전히 작은 규모의 네트워크
  • 숫자데이터는 단순한 수준에 불과

 

 

 

 

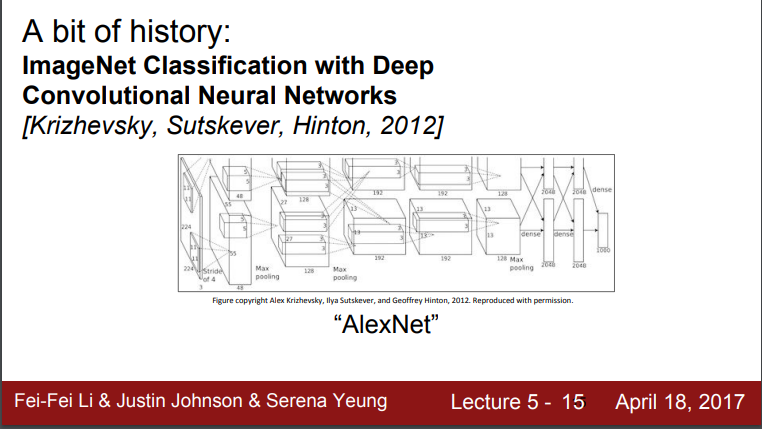
• 2012년 Alex Krizhevsky의 CNN 현대화 - AlexNet 대두
• 기존과 구조는 비슷하나 더 크고 깊어진 구조
• 대규모의 데이터 처리 가능(GPU의 병렬처리 기능 향상도 영향을 줌)

 

 

 

 

 

---

CNN usage

CNN은 어떤 곳에 사용될 수 있는가?

 

특징이 유사한 것들을 매칭시키는데 매우 강력함

 

Detection분야에서도 사용 - segentation(픽셀 하나하나 모두 레이블링)

 

자율 주행에 사용 - 우측의 GPU가 병렬처리로 이미지 디텍션을 굉장히 빠른 속도로 진행함

 

얼굴 인식으로 어떤 사람인지 인식하는 것을 맞춤, 비디오도 가능

pose recognition 도 가능

의학영상 예상, 은하 분류, 표지판 인식 등에도 사용

고래 인식, 항공지도로 길과 건물 인식 등

추가 : 이미지 captioning - 이미지 설명하기

예술작품 만들기 - style transfer는 원본 이미지를 가지고 특정 화풍으로 다시 그려줌

---

How CNNs work?

Convolution Layer

fully connected layer와 convolution layer 

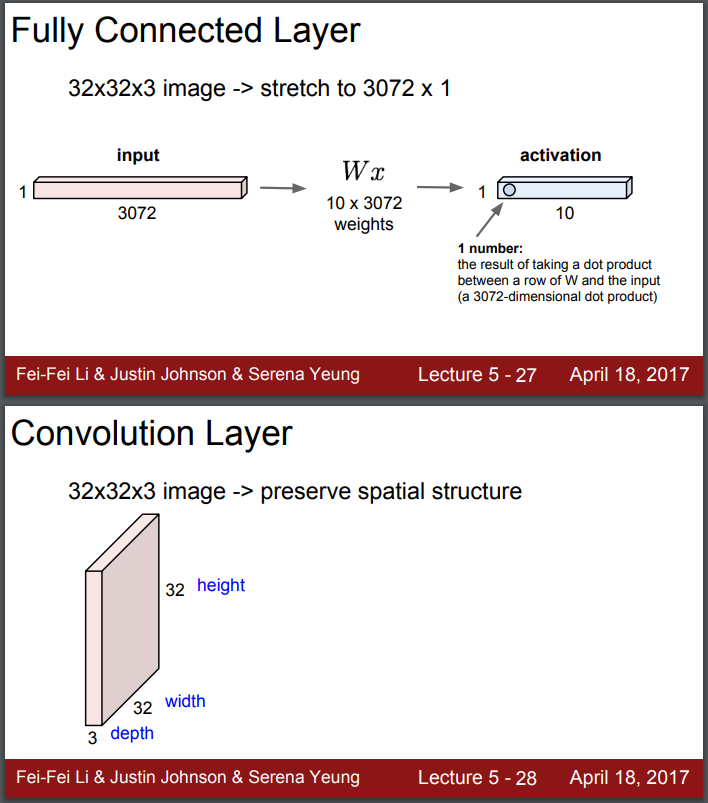
• Fully connected layer - 이미지를 길게 펴서 3072차원의 긴 벡터로 만들고, 해당 길이에 적합한 웨이트와 내적을 통해 activation을 얻음 : 이미지를 flatten 시키는 과정에서 기존 구조정보가 손실된다는 단점
• Convolution layer - 이미지 구조를 그대로 가져와 기존의 구조를 보존시킴. 

 

Filter - 가중치를 가진 필터가 이미지를 슬라이딩하며 내적 연산을 함.

필터는 대상 사진 이미지에서 자기 자신의 크기만큼의 픽셀 값과만 내적 연산을 실시 - 단, 깊이는 반드시 다 취해줌.

 

 

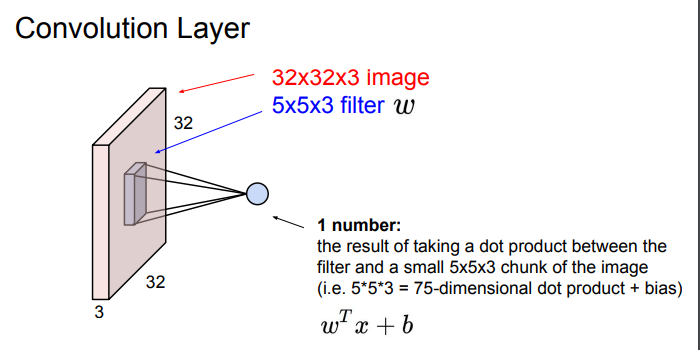
해당 필터가 전체 이미지에 내적이 되는데, 필터의 각 w와 해당하는 이미지의 픽셀을 곱한다. b는 bias.\

 

 

Q1. 실제 필터로 내적을 할 떄에는 5x5x3짜리 긴 벡터를 사용하는가?
A1. 그렇다. 각 원소간 convolution = 두 벡터 flatten 후 내적

Q2. w를 왜 transpose 하는가?
A1. 내적을 수학적으로 나타내기 위한 표현 방식일 뿐, 단지 w 표현 방식의 차이다. 행 백터를 만들어주기 위해 T 하는 것.

Q3. w는 그러면 1x75짜리 벡터인가?
A3. 그렇다. 내적 수행을 위해 일단 w를 길게 펴야한다. 해당 이미지는 보기 편하라고 저렇게 표현한 것 뿐이고, 실제로는 모두 펴서 벡터간의 내적을 구하는 것이다.

Q4. convolution이면 뒤집어서 연산되는게 맞지 않나?
A4. 그렇다. 그렇지만 여기선 신경쓰지 않아도 된다. CNN에선 의미적 요소만 가져온 것이기 때문(?) - 무슨말?

 

Filter sliding

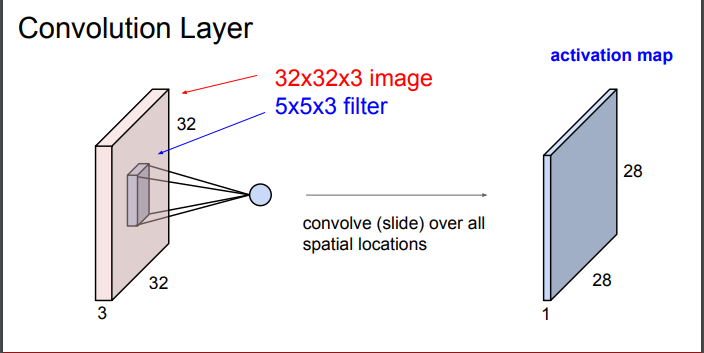
• 필터는 이미지의 좌상단부터 컨볼루션을 시작함
• 필터가 이미지에 한번 내적될 때 값 하나 산출 - 필터의 모든 가중치들과 내적을 수행해 하나의 값을 얻음
• 값을 얻은 뒤 필터가 옆으로 슬라이딩해 다시 컨볼루션을 통해 하나의 값 산출
• conv 연산 수행된 값은 output activation map에 해당하는 위치에 저장됨 - 입력행렬과 출력행렬 사이즈가 다름
  • 출력행렬의 크기는 슬라이드 방식에 따라 달라짐 - 조절 가능

 

• 해당 그림처럼 여러 개의 필터를 사용함 - 필터마다 다른 특징 추출하기 위해
• 각 필터마다 각각의 출력 map 만듦 : 필터 갯수 = activation map 갯수

 

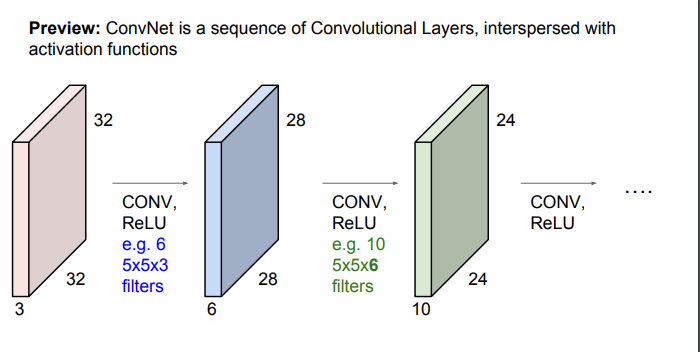
• 입력행렬 -> CONV(with filter) + ReLU -> 출력행렬 -> CONV(with filter) + ReLU -> 출력행렬 -> .... 반복

 

 

여러 개의 layer를 쌓으면, 계층적으로 학습하는 필터들 관측 가능! 

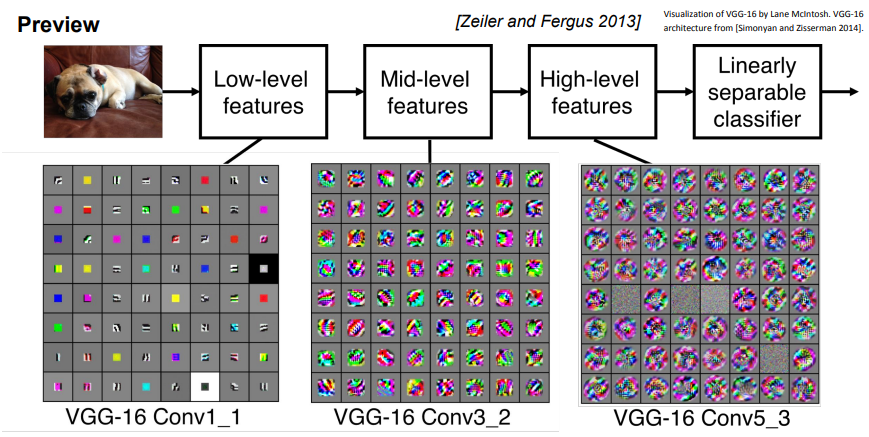
• 앞쪽에 위치한 layer들은 단순한 Low-level features(edge 등)을 학습
• layer 층이 깊어질수록 더 자세하고 복잡한 features 학습
•  

 

 

정리 : Conv layer를 계층적으로 쌓아 단순한 특징을 뽑고 그것을 또 조합해 더 복잡한 특징으로 활용

강제로 학습시킨 것이 아니라 계층적 구조를 설계하고 역전파로 학습시키니 필터가 이런식으로 학습이 된 것!

Q1. 필터의 depth를 늘리는데 어떤 직관을 가져야 하는가?
A1. 모델 디자인에 관련된 내용인데, 실험해보는 수밖에. 기본적으로 아주 다양하게 CNN 디자인 가능하다!

Q2. 이미지를 슬라이딩하며 필터링을 하는데 이미지의 가장자리는 필터가 덜 적용되는 것이 아닌가?
A2. 그렇다. 그것을 보완하기 위해 하는 작업을 앞으로 알아볼 것이다.(zero padding과 같은 방법 이용)

Q3. 사진에서 시각화된 것은 무엇인가?
A3. 각 그리드의 요소가 하나의 필터. 이미지가 어떻게 생겨야 해당 필터의 활성화를 최대화시킬 수 있는지 나타낸 그림이다. 시각화를 위핸 backprop 필요.

 

 

EX of activation map

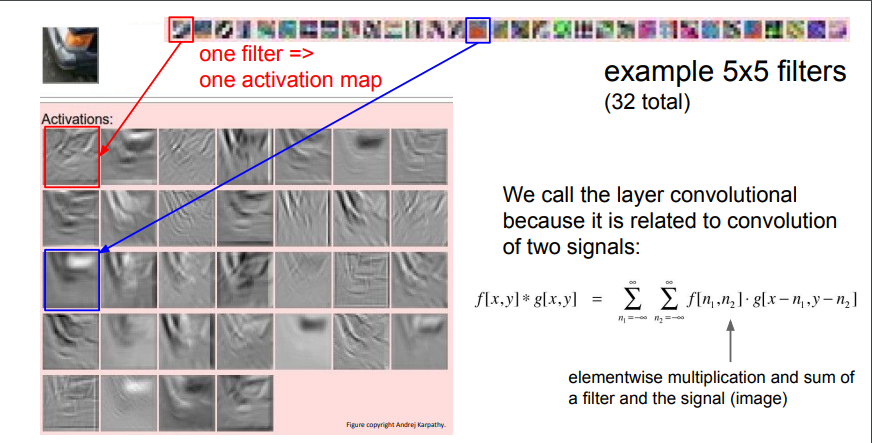
• 자동차 한 부분 이미지에 대한 5x5 필터 32개의 activation map 결과양상 : 이미지 중 어느 위치에서 각 필터가 크게 반응하는지 보여줌

 

• 붉은색 필터는 은 edge를 찾고 있다. - 해당 필터를 슬라이딩 시키면 이 필터와 비슷한 값들은 값이 더 커지게 됨

and if u slide over the image, it will have a high value, a more white value where there are edges in this type of orientation

(이것도 웨이트 업데이팅인건가? 이 필터와 비슷한 어디의 값들이라는 거지?)

 

 

 

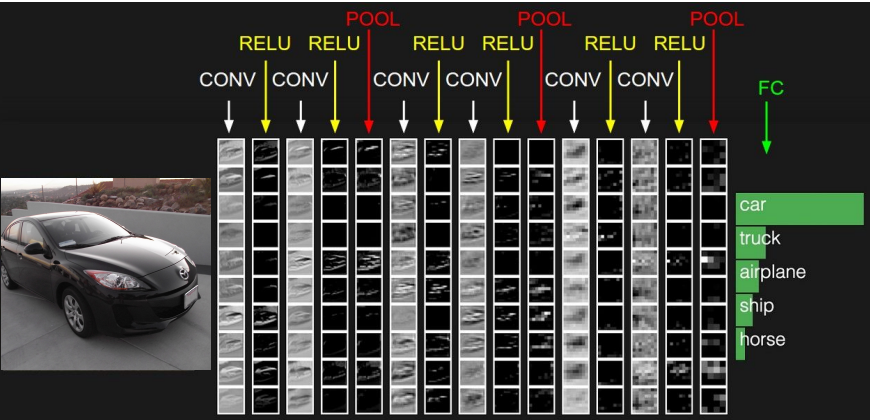
CNN 전체 과정

CONV -> nonlinear func(ReLU in general) -> CONV -> nonlinear func(ReLU in general) -> POOL(activaiton map downsizing) -> ...iter -> FC(score mearsure)

 

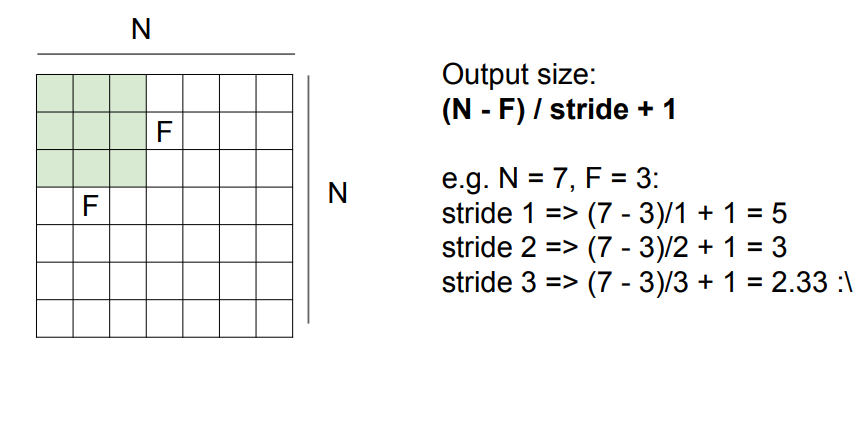
spatial dimensions

깊이를 제외한 필터나 이미지의 크기를 의미

해당 7x7 spatial dim에서 3x3 필터가 1씩 sliding : 좌우방향으로 5회, 상하방향으로도 5회 움직임

-> 5X5 activation map 산출

 

 

stride?

• 필터가 sliding하는 보폭
• stride = 1일경우 한칸씩 옆으로 움직이며, n일 경우 n칸씩 건너뛰며 sliding한다.
• stride는 필터와 이미지의 spatial 크기에 맞게 잘 설정 해 줘야함!

해당 경우처럼 공간 크기에 안맞는 stride를 설정하면 전체 이미지를 다 커버할 수 없기 때문에 설정에 주의해아함.

 

 

입력차원과 필터크기, stride에 따른 activation map 차원 계산 공식

해당 식에서 정수로 나누어떨어지지 않는 경우는 fllter가 이미지를 다 커버하지 못한다는 뜻 - 재조정 필요

 

 

 

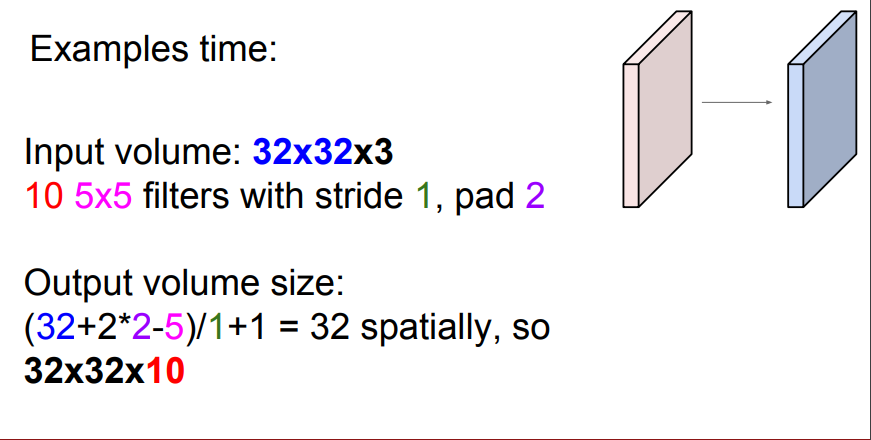
Zero padding - input matrix 가장자리에 0 값을 채워넣는 행위

• 목적
  • 출력차원 크기 원하는대로 조절하기 위함 (주로 필터 연산 이후에도 input image 와  output image의 size를 같게 유지하기 위함)
    • 패딩을 주지 않으면 필터 연산을 할 때마다 출력값은 점점 작아질 것이고, 이는 정보 손실을 의미한다.  원본 이미지를 표현하는데 충분치 않은 너무 작은 값을 이용해 인식 정확도가 떨어질 수 있다.
  • 필터가 닿지 않는 가장자리 부분의 정보 더 잘 인식하기 위함

해당 그림처럼 패딩하면 인풋과 아웃풋 차원을 똑같게 유지할 수 있다.

 

Q1. 실제 출력값은 7x7x3 인가?
A1. 실제 출력값은 7x7xfilter 갯수이다. 각 필터가 입력의 모든 깊이에 내적을 수행하므로, 깊이가 3이라도 하나의 값만 나온다.

Q2. input이 32x32x3처럼 depth가 있는 예제에서는 어떻게 적용되는가?
A2. 필터에 depth만큼을 곱해주면 해당 예제에서의 필터 차원이 정의된다. 위의 예제에서는, 3x3xdepth차원 이다.   

Q3. Zero padding 을 해주면 모서리에 필요없는 특징을 추가하는 것이 아닌가?
A3. 목적은 영상 내 어떤 모서리 부분에서 값을 얻고 싶은 것이다. zero padding은 그 중의 한 방법이다. zero padding을 통해서 우린 기존에는 필터가 닿지 않았던 영상의 모서리 부분에서도 값을 뽑을 수 있게 된다. 물론 모서리부분에 약간의 오차가 발생하지만 대부분 경우 잘 작동한다. 

Q4. 사진이 정방형이 아닌경우는 수직, 수평방향의 stride를 다르게 주면 되나?
A4. 그렇다. 하지만 주로 정방형의 사진으로 가공후 같은 stride를 이용한다.

 

 

 

예제

(32+2*2) - 5/1 +1 = 32

bias는 각 필터당 연산 이후 더해지는 숫자 -> 필터 수만큼 존재

 

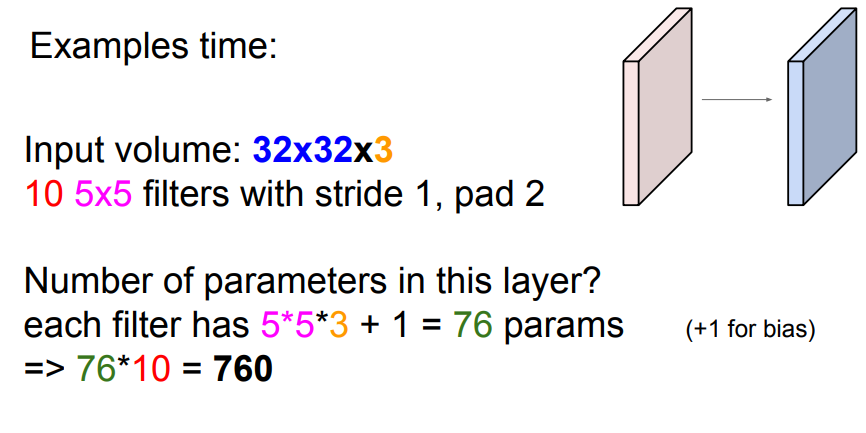
common settings in CNN

• 필터갯수는 주로 2의 배수로 설정한다
• stride는 주로 1이나 2로 설정한다

 

 

1x1 conv layer의 의미 - 입력의 전체 depth에 대한 내적 수행

 

 

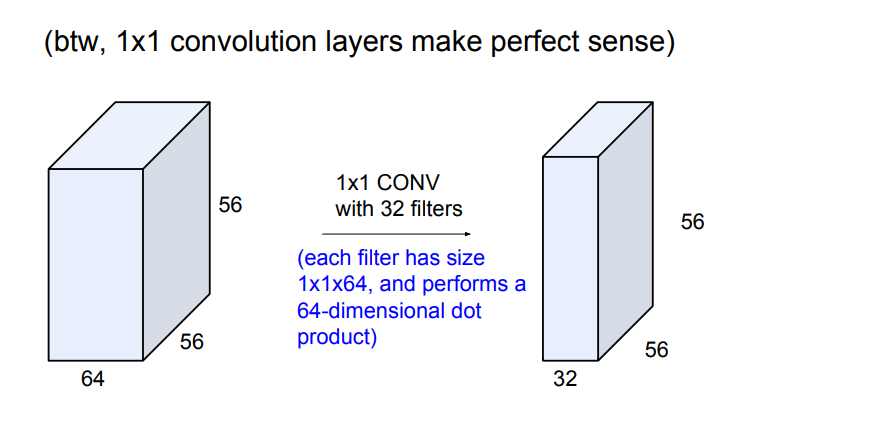
Q1. Stride를 어떤식으로 결정해아하는가?
A1. Stride를 키우면 키울수록 output 이미지는 작아짐. 이는 pooling을 통한 다운샘플링과 비슷한데 주로 pooling보다 더 좋은 성능을 보임.  다운샘플링의 이유는 전체 파라미터 갯수를 줄일 수 있기 때문. 마지막에 FC에서는 모든 Conv 출력값과 연결되어 있기 때문에, 최종 출력값이 작을수록 필요한 파라미터 갯수가 줄어든다. 이와 같이 파라미터 수와 더불어 모델의 크기, overfitting등을 모두 고려해 stride를 설정해야한다.

---

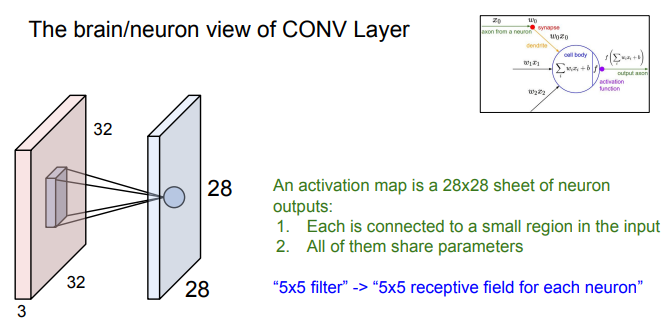
convolution layer가 뉴런과 다른점

-Conv는 슬라이딩을 하며 모든 이미지를 다 봄. 즉 같은 가중치 값을 지닌 필터를 슬라이딩 하며 계속 이용 

- 뉴런은 Conv layer와는 다르게 특정 부분에만 연결되어있음. 즉 하나의 뉴런은 한 부분만 처리하고, 이런 뉴런들이 모여 전체 이미지를 처리하는 것. 이러한 방식으로 saptial structure를 유지한 채로 activation map 생성

 

- 그러니까, 뉴런은 (한 이미지 정보에 대해) 필터 하나를 한번만 쓴다는 걸로 이해하면 되는건가?

 

 

 

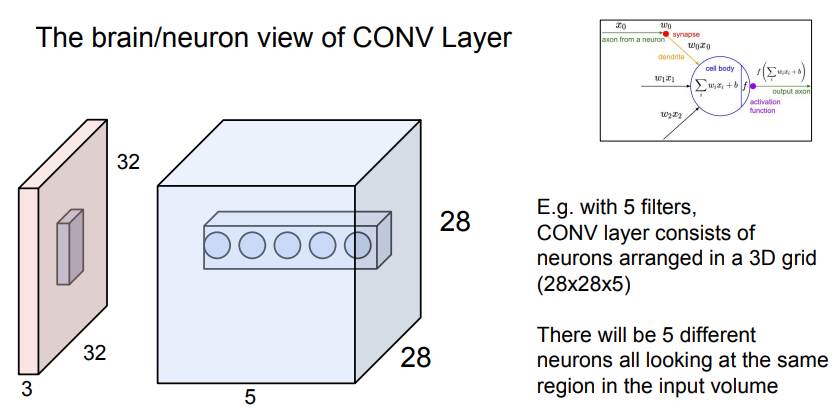
파란색 : 필터 5개로 만든 activation map 5개

• 해당 activation matrix에서 깊이방향으로 원소를 보면 정확히 같은 부분의 입력이미지에서 추출한 서로 다른 특징 5개를 나타냄. -> 각 필터는 이미지에서 같은 곳을 봐도 다른 특징을 추출한다!

Q1. layer에서 filter가 하는 일은 항상 동일한가?
A1. 그렇다. 슬라이딩 마다 같은 연산을 수행하고, 결괏값을 산출한다.

---

 

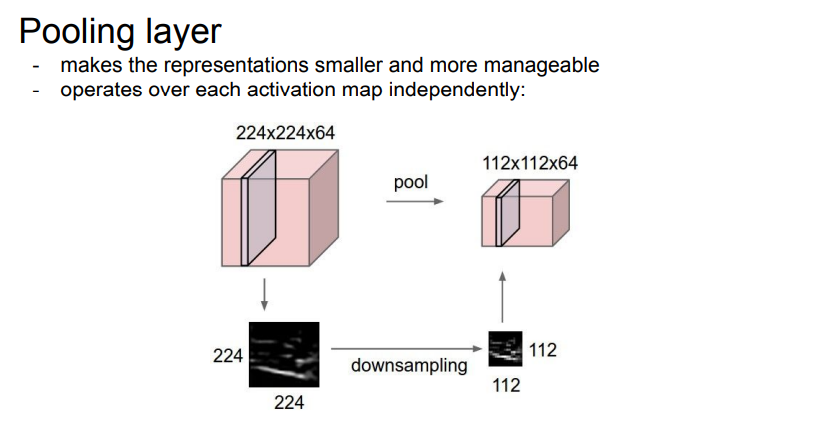
• 표현된 결괏값들을 더 작고 관리하기 쉽게 만들어주는 역할을 하는 downsampling layer
• 작아지면 파라미터 수 감소, 공간적 불변성 취득 가능(?)
• depth는 건드리지 않음
• Max pooling이 주로 사용

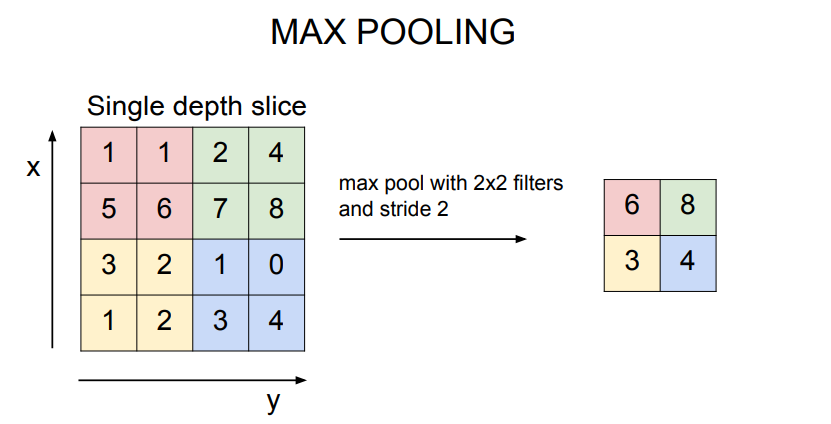
슬라이딩 하며 연산을 수행하는 것은 같으나, 마지막에 내적이 아닌 가장 큰 값을 추출함

Q1. pooling시 filter의 receptive field가 겹치지 않는 것이 관례인가?
A1. 그렇다. 목적이 downsampling이기 때문에 한 지역에서 하나를 뽑고, 겹치지 않는 다른 지역에서 하나를 뽑고 하는 방식이 이치에 맞다. 

Q2. max pooling이 더 좋은 이유는?
A2. 우리는 얼마나 이 뉴런, 즉 필터가 활성화되었는지를 나타내는 값들을 activation map에 나타내었다. Max pooling은 그 지역이 어디든, 어떤 신호에 대해 "얼마나"그 필터가 활성화 되었는지를 알려준다, 인식의 관점에서, 그 값이 어디에 있었는지보다 얼마나 큰지가 더 중요하다. ??무슨말?

Q3. 도대체 pooling이나 stride나 뭐가 다른가? 같은 효과지 않나?
A3. 그렇다. 요즘들어 사람들이 Downsample할때 pooling을하기보단 stride를 많이 사용하고 있는 추세다. stride로 downsizing해도 문제 없다.

 

일반적인 세팅

- pooling layer에서는 보통 padding을 하지 않는다. 왜나하면 우리는 downsampling이 목적이고, 또한 Conv 때처럼 코너의 값을 계산하지 못하는 경우도없기 때문이다. 

 

---

CNN 마지막 - fully connected layer

CNN layer 에서 출력된 3차원 값을 1차원 vector로 flatten 시킨 뒤 이를 FC layer의 입력으로 사용함

 

Q1. 각각의 열을 어떻게 해석해야하는가?
A1. 각각의 열은 activation map들을 의미한다. 

Q2. 결괏값을 보면 굉장히 적은 양의 정보만 담고 있는 것처럼 보이는데 저걸로 판단을 어떻게 하는가?
A2. 오른쪽 맨 끝의 출력값은 전체 네트워크를 통과한 집약체이다. 계층구조의 최상위이며, 가장 복잡한 feature들을 다 담고있다.  기존 단계에서 추출한 저수준의 특징 맵들을 이용해 더 자세한 특징을 파악하고, 그렇게 파악한 특징들로 더 자세한 특징들을 다시 파악하는 방식이기 때문에 후반부의 출력은 가장 자세하고 필수적인 정보들을 담고 있다. (각 값들이 의미하는 것은 필터의 Templete이얼마나 활성화 되었는가를 의미하는 것)