딥러닝 알고리즘의 구현 방식, 신경망에 대해 알아보자.
신경망(Neural network)이란?
우리 뇌에는 1000억 개에 가까운 신경계 뉴런들이 있다. 이 뉴런들은 서로 매우 복잡하게 얽혀 있고, 조금 물러서서 보면 하나의 거대한 그물망과 같은 형태를 이루고 있다. 보통 우리는 이를 신경망이라고 한다.
머신러닝/딥러닝 분야는 위와 같은 뇌 속의 신경망처럼 컴퓨터 알고리즘을 구현하여 인공지능을 만들고자 시도했다. 그들은 우리 뇌 속의 신경망 구조에 착안해서 퍼셉트론(Perceptron)이라는 형태를 제안하며 이를 연결한 형태를 인공신경망(Artificial Neural Network)이라고 부르기 시작했다.
다층 퍼셉트론

- 입력층(input layer), 은닉층(hidden layer), 출력층(output layer) 으로 구성
- 2개 이상의 레이어가 쌓여 만들어진 것을 다층 퍼셉트론(Multi-Layer Perceptron; MLP)이라고 부름
- 은닉층이 많은(깊은) 인공신경망을 DNN(Deep Neural Network)라고 함
Parameters/Weights
입력층-은닉층, 은닉층-출력층 사이에는 사실 각각 행렬(Matrix)이 존재
이러한 행렬들을 파라미터(웨이트 + bias) 혹은 weight라고 부름

예시
- 입력값이 100개, 은닉 노드가 20개라면 사실 이 입력층-은닉층 사이에는 100x20의 형태를 가진 행렬이 존재
- 10개의 클래스를 맞추는 문제를 풀기 위해 출력층이 10개의 노드를 가진다면 은닉층-출력층 사이에는 20x10의 형태를 가진 행렬이 존재
활성화함수 (Activation Function)
- 비선형 함수를 MLP 안에 포함시키면서 모델의 표현력이 좋아지게 된다.
- 레이어 사이에 이 비선형 함수가 포함되지 않은 MLP는 한 개의 레이어로 이루어진 모델과 수학적으로 다른 점이 없다. 아무리 함수 안에 함수를 넣는 식으로 레이어를 깊게 만들어도 결국엔 하나의 함수로 정의되는거나 마찬가지이기 때문 -> f1(f2(f3(f4(X))) = g(X) 처럼 나타낼 수 있는것처럼
활성화 함수 01. - Sigmoid Function

- 모든 값을 0~1 사이 값으로 바꾸어준다.
- vanising gradient 현상이 발생
- exp 함수 사용하기때문에 비용 大
활성화 함수 02. - Tanh

- 모든 값의 범위를 -1~1로 바꿈
- tanh 함수는 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결.
- vanishing gradient 문제 존재.
- 소프트맥스(softmax)기법에 사용(n개중 하나일 확룰로 변경)
활성화 함수 03. - Relu

- sigmoid, tanh 함수에 비해 학습이 빠름.
- 연산 비용이 크지 않고, 구현이 매우 간단하다.
- vanishing gradient 발생 x
손실함수(Loss Function)
비선형 활성화 함수를 가진 여러 개의 은닉층을 거친 다음 신호 정보들은 출력층으로 전달. 이때 우리가 원하는 정답과 전달된 신호 정보들 사이의 차이를 계산하고, 이 차이를 줄이기 위해 각 파라미터들을 조정하는 것이 딥러닝.
이 차이를 구하는 데 사용되는 함수가 손실함수(Loss function) 또는 비용함수(Cost function)
손실함수 01. - 평균 제곱 오차(MSE : Mean Square Error)
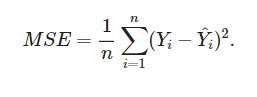
손실함수 02. - 교차 엔트로피 (Cross Entropy)
- 두 확률분포 사이의 유사도가 클수록 작아지는 값(예측값과 정답값이 비슷할수록 값이 작아짐)
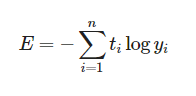
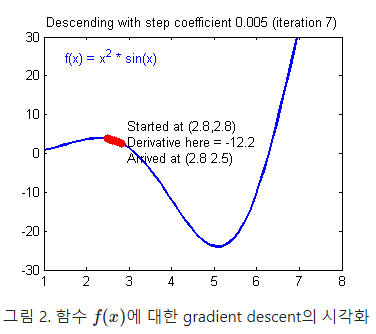
경사하강법(Gradient Descent)
- 파라미터의 최적값을 찾기 위해 Loss function의 최소지점의 파라미터 값을 찾는 방식 中 하나.
- 주로 분석에서 만나는 함수는 비선형함수인 경우가 많아 미분계수, 근을 구하기 힘듦.
- 따라서 x값을 조금 옮겼을떄의 값 변화로 기울기의 방향을 파악한다.
- <방식>
- 손실함수 값이 작아지면 기울기가 음수(하강중), 높아지면 기울기가 양수(상승중)
- 손실함수 값이 작아지는 쪽, 즉 음수방향의 값으로 이동한다. (이동 거리는 learning rate값으로 조정)
- 이동해도 더이상 값 변화가 없으면, 즉 미분계수가 0인 지점, 최소지점 - 멈춘다.
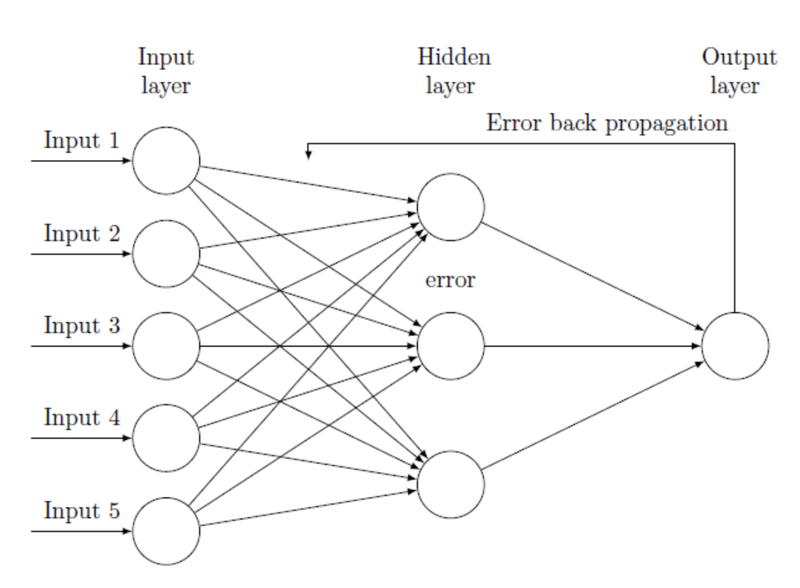
경사하강법으로 구한 기울기를 입력층까지 전달하는 방식
오차역전파법(Backpropagation)
출력층의 결과와 내가 뽑고자 하는 target 값과의 차이를 구한 뒤, 그 오차 값을 각 레이어들을 지나며 역전파 해가며 각 노드가 가지고 있는 변수들을 갱신
'Computer Technology 기록부 > 인공지능 학습 기록부' 카테고리의 다른 글
| CS231n Lecture 05. CNN - Convolution Neural Network (0) | 2022.02.06 |
|---|---|
| CS231n Lecture 04. Introduction to Neural Networks (0) | 2022.01.28 |
| 딥러닝과 신경망의 본질 (0) | 2022.01.20 |
| CS231n lecture 03 Loss function and optimization (0) | 2022.01.17 |
| CS231n Lecture 02 Image Classification (0) | 2022.01.11 |




댓글