Topic : How to choose weight for best accuracy
Loss function
- w가 얼마나 좋은지 나쁜지를 결정하는 함수. 가장 덜 나쁜 w는 무엇인지를 결정하는 함수 - 최적화 과정
General formulation to determine Loss
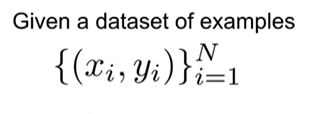
- x : image, y : label(how many classes exist in data), N : number of image
- f : Loss function, W : weight, L : Loss
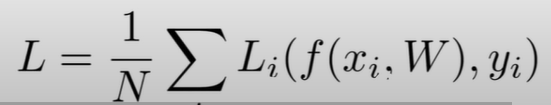
- Minimize the value L is the way to optimize algorithm
Loss function 1. Hinge loss in Multiclass svm loss
(이미지내 정답이 아닌 카테고리의 점수 - 이미지 내 정답인 카테고리 점수 +안전마진)들의 합 = 한 이미지의 최종 Loss
- 올바른 카테고리점수가 틀린 카테고리 점수보다 안전마진(safe margine)보다도 크면 loss는 0

- hinge loss(경첩 손실함수) : sj + 1을 넘어가면 loss가 0이 되는 것을 볼 수 있다.
- s : 분류기의 출력으로 나온 예측된 스코어
- s_j : j번째 클래스로 예측된 스코어
- s_y_i : i번째 이미지의 정답 클래스로 예측된 스코어
정답스코어는 다른 클래스 스코어보다 훨씬 더 높아야 loss가 줄어든다는 사실을 알 수 있음

트레이닝 데이터에서 Loss를 최소화하면 안되는 이유
- Over fitting
트레이닝 데이터의 loss를 최소로 만들기 위한 튜닝을 한다면(가령, 위의 식에선 w를 2배하는 식의 방식 - loss함수에서 0으로 가는 항들이 더 많아지게됨) loss는 줄어들게 되겠지만 테스트셋에서는 더 낮은 성능을 보일것이다
- 해결책 - Regularization 함수 추가 - 트레이닝 데이터 셋에 완벽히 핏하지 못하도록 모델의 복잡도에 패널티 추가
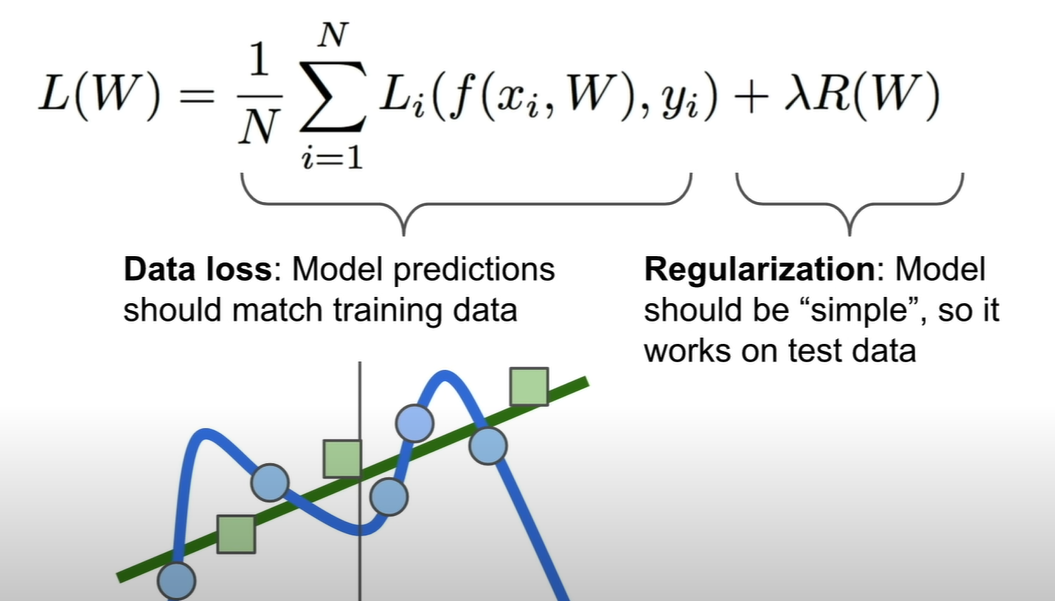
모델을 단순화하기 위해 다차항식을 더 저차원의 식으로 패널티를 줘 줄임으로서 함수를 더 일반화시키고, 간단하게 만드는 것
L1 regularization vs L2 regularization

"복잡하다"의 측정 방식 차이
- L1 : 0이 아닌 w의 요소들의 갯수가 많을수록 복잡합
- L2 : w의 요소들의 분산 정도가 낮을수록 복잡함
- 주로 모든 웨이트에 가중치가 붙은 경우를 L2가 더 선호함.
- L2는 모든 x의 요소가 골고루 영향을 미쳤으면 한다.
Loss function 2. cross-entropy loss in Softmax classifier
분류기를 통해 산출된 결괏값 스코어(e^정답클래스 스코어/e^모든 클래스 스코어들의 합 )에 log를 취하고 -를 붙임(loss는 얼마나 안좋은지를 판단하는 것이므로 -를 붙임)

- 초기 클래스 점수에서 지수화를 시켜 모두 양수값으로 만들고, 편차를 심하게 하여 값을 과장시킨 뒤, nomallize를 통해 모든 값의 합을 1이되게 만든다. 그후 -log를 취해 손실값을 구한다.
Review

Optimization : how do we actually find W that minimize the loss
loss의 최솟값을 명시적 솔루션, 계산을 통해 구하기엔 굉장히 복잡한 다차원식인 경우가 많다.
- Random search - possible, but inefficient
- Follw the slope - follow the down hill
- slope? : derivative of a function(gradient)
- if derivative of a function is 0 : reach flat area(can be minimum loss, cannot 100% sure)
Numerical gradient : approximate, slow, easy to write
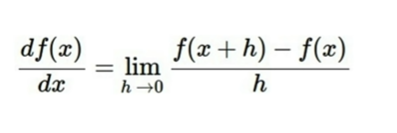
첫번쨰 w에 굉장히 작은 숫자를 더한 값의 loss를 기존의 loss와 비교하고, 위의 극한식을 이용하여 근사시킨 gradient를 구한다. 이후 첫번쨰 w를 다시 원래대로 돌려놓고, 두번째 w에 다시 위의 절차를 반복한다. 이렇게 모든 웨이트들에서의 gradient를 구한다. -> 매우 복잡하고, 느리고, 정확하지 않지만 디버깅에 유용하다.

Analytic gradient : exact, fast, error-prone

식 하나로 계산할 수 있기 때문에 훨씬 빠름. 해당 함수의 gradient를 나타내는 식이 뭔지 먼저 찾아낸 후, 수식으로 나타낸 후 미분하여 바로 계산해 냄. 실제로 주로 이 방식을 이용함.
Gradient Descent

음수의 기울기값을 계산하고, step size만큼 기울기 음수 방향으로 이동하며 가장 낮은 지점알때의 w1, w2의 값을 찾기
소제목6
- 문제점 - gradient descent를 위해 모든 데이터의 loss를 구하고, 평균을 구하는데는 시간이 많이 걸림. 특히 N의 값이 클 경우 더욱
- 해결방안 - mini batch를 이용하여 데이터 중 일부끼리 그룹화 한 뒤, 그 안에서 loss와 gradient를 계산하고 w를 업데이트한다, 이것을 Stochastic Gradient Descent(SGD)라고 한다.

Feature vector 산출 방식 (before NN)
- color histogram(각 픽셀들의 색상값으로 판단)
- HOG(픽셀들의 값 변화량으로 판단)
- bag of words(visual word로 이미지 패치를 뽑아내 분류)
- NN 들의 방식은 어떠한 룰에 의해 특징을 먼저 뽑아내고, 그렇게 뽑아 낸 특징벡터를 분류기에 넣는 기존 방식과는 달리 raw데이터가 직접 들어가 여러 은닉층을 거치며 특징표현 뽑아낸다. 따라서 한번 뽑은 특징벡터가 계속 업데이트된다는 차이점이 있다.

'Computer Technology 기록부 > 인공지능 학습 기록부' 카테고리의 다른 글
| CS231n Lecture 05. CNN - Convolution Neural Network (0) | 2022.02.06 |
|---|---|
| CS231n Lecture 04. Introduction to Neural Networks (0) | 2022.01.28 |
| 신경망(Neural Network)이란? (0) | 2022.01.25 |
| 딥러닝과 신경망의 본질 (0) | 2022.01.20 |
| CS231n Lecture 02 Image Classification (0) | 2022.01.11 |




댓글